Tycoon-style Terrain

posted March 25, 2018

RollerCoaster Tycoon (and the other similar Tycoon games) had a distinct terrain style, something like this:

Basically, it’s a like a heightmap, except tiles can be extruded if the difference between neighbor heights is not the same. In the case of this terrain, a tile is a collection of four distinct points on the terrain.

In my implementation, I have a basic Tile object which has a few properties:

topLeft, topRight, bottomLeft, bottomRight: Absolute heights of the tile. These are clamped so all values are -/+ one of the other.
flat, edge: An index into a tile set representing the type of tile rendered. The tile set stores properties like texture and color.

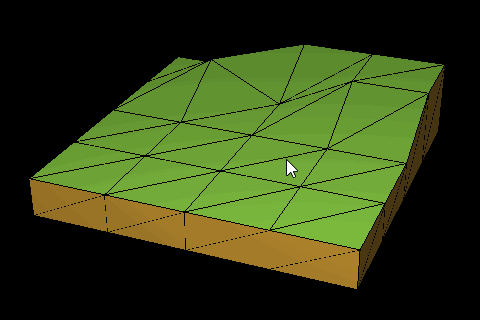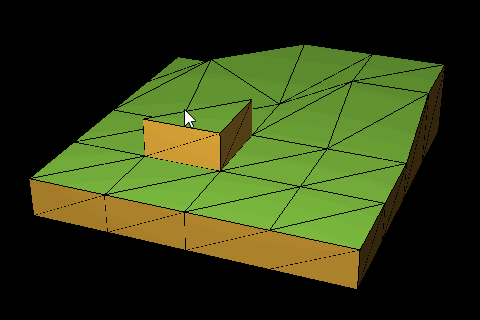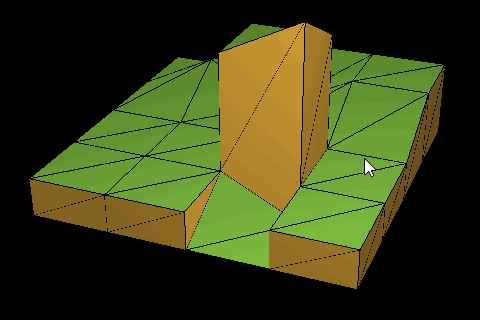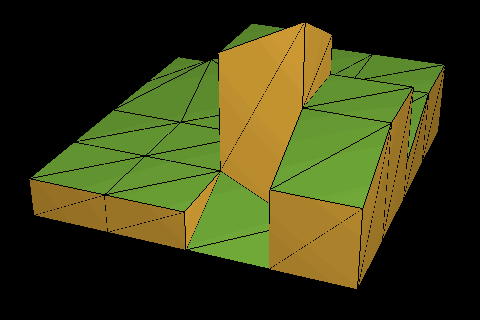
And a map (or Stage in my case) is a collection of these tiles. A 4 × 4 map is thus equivalent to an 8 × 8 heightmap. The biggest different is when the heights of neighbor points diverge, the tile appears extruded and a wall/edge is generated (see image above).

The triangulation process is simple enough. The tiles can be triangulated easily enough: in my case, I form two triangles: (topLeft, topRight, bottomRight) and (topLeft, bottomRight, bottomLeft). The edges, however, are a bit trickier.

Here’s a sample that generates the vertices for a left edge:

local function getLeftVertices(tile, neighbor) local tileRef1 = tile.topLeft local tileRef2 = tile.bottomLeft local neighborRef1 = neighbor.topRight local neighborRef2 = neighbor.bottomRight local difference1 = tileRef1 – neighborRef1 local difference2 = tileRef2 – neighborRef2



  local t
  if difference1 >= 1 and difference2 >= 1 then
    t = {
      Vector(-1, tileRef1, -1),
      Vector(-1, tileRef2, 1),
      Vector(-1, neighborRef2, 1),
      Vector(-1, tileRef1, -1),
      Vector(-1, neighborRef2, 1),
      Vector(-1, neighborRef1, -1)
    }
  elseif difference1 >= 1 then
    t = {
      Vector(-1, tileRef1, -1),
      Vector(-1, tileRef2, 1),
      Vector(-1, neighborRef1, -1)
    }
  elseif difference2 >= 1 then
    t = {
      Vector(-1, tileRef2, 1),
      Vector(-1, neighborRef2, 1),
      Vector(-1, tileRef1, -1)
    }
  end

  return t, Vector(-1, 0, 0), Vector(0, 0, 1)

Essentially, the logic is: if both reference points (e.g., tile’s topLeft and neighbor’s topRight) are separated by more than 1 unit, it’s considered separate and a triangle needs to be added. There’s three cases: both corners are separate, the first corner is separate, and the second corner is separate.

Of course, we could just brute-force it and add 0-area triangles, but what’s the fun in that? :)

The logic for the other edges are the same, just rotated. I couldn’t think of a nicer way of handling it without creating some weird metafunctions, so I just hardcoded the four permutations (left, right, top, bottom).

(Note: Units are rounded to the nearest integer, so fractional elevations aren’t allowed).

In the end, it creates something nice: